개요
https://www.acmicpc.net/problem/13016
13016번: 내 왼손에는 흑염룡이 잠들어 있다
첫째 줄에 국가의 수 N(2 ≤ N ≤ 50,000)이 주어진다. 둘째 줄부터 N-1개의 줄에 도로의 정보가 주어진다. 각 도로의 정보는 from, to, length 으로 이루어져 있으며, 이 도로는 국가 from과 국가 to를 연결
www.acmicpc.net
PlatinumV
문제 제목이 왜 이래
풀기 전, 선행하면 좋은 문제 1667번: 트리의 지름
풀이
대충 요약하자면 , , 가중치가 있는 트리의 모든 노드에서 가장 먼 노드까지의 거리를 출력하면 된다.
N<=50000 이기 때문에 당연하게도 모든 노드에서 가장 먼 노드를 탐색(DFS)하면 시간 초과가 난다.
우선 두가지 아이디어가 떠올랐다.
첫 번째 아이디어는 모든 노드에 DFS를 수행시키며 한 번 지나간 간선에 최장거리를 저장하며 탐색하는 것이다.(DFS 최적화?)
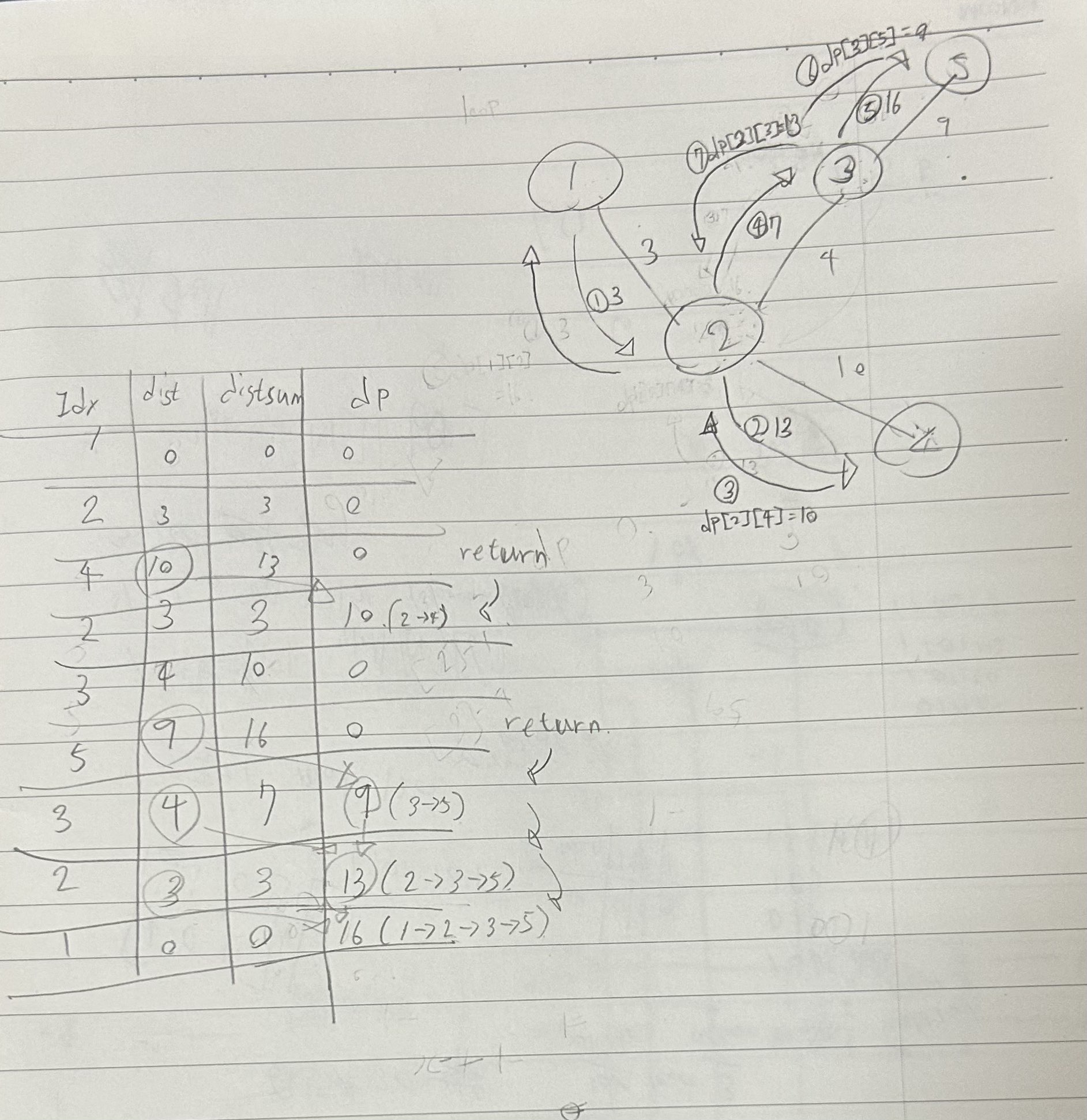
재귀로 DFS를 수행하며 리프 노드에 도달 했을 때 리턴하며 거리를 저장했다. 다시 해당 간선을 지나가려고 하면 저장된 거리 값만 가져오면 될 수 있도록했다. 결과는 , , ,
시간 초과가 나버렸다.
87%라 최적화하면 될 것 같았는데 이게 안되네 ,, 해당 코드
시간이 아깝긴 했지만 아무리 최적화 해도 안되는걸 확인하곤 두 번째 아이디어로 진행했다.
두 번째 아이디어는 DFS로 리프노드를 두개 찾고 해당 노드들에서 각 노드별 거리를 측정하는 것이었다.
이는 이전에 배우면서 풀었던 1667번: 트리의 지름 에서 사용했던 테크닉이다.
우선 임의의 노드에서 DFS로 최장거리에 있는 리프 노드 하나를 탐색한다.
그 후 해당 리프노드에서 한 번 더 DFS를 하면 최장거리 리프 노드 두개를 찾아 낼 수 있다.
모든 노드에서 가장 먼 거리의 노드는 위의 두 리프 노드 중 하나다. (이게 확신이 안서서 첫 번째 아이디어를 먼저 구현했다,,)
두번의 DFS를 하는 동안 지나는 노드들의 거리 값중 최고 값을 해당 노드에 저장했다.
이렇게 하면 모든 노드에 최장거리 값이 저장되게 된다.

정말 굉장히 재밌고 유용한 테크닉이다,,!
코드
#include <bits/stdc++.h>
using namespace std;
constexpr int LIMIT = 50001;
struct Node {
int idx;
int dist;
};
int N;
vector<Node> graph[LIMIT];
bool visited[LIMIT];
int result[LIMIT];
int startNode;
int maxSum;
void dfs(int idx, int distSum=0)
{
visited[idx] = true;
if (distSum > maxSum)
{
maxSum = distSum;
startNode = idx;
}
result[idx] = max(result[idx], distSum);
for (int i = 0; i < graph[idx].size(); i++)
{
auto& [nIdx, dist] = graph[idx][i];
if (visited[nIdx]) continue;
visited[nIdx] = true;
dfs(nIdx, distSum+dist);
}
}
int main() {
cin.tie(0)->sync_with_stdio(0);
cin >> N;
for (int i = 1; i <= N-1; i++) {
int from, to, dist;
cin >> from >> to >> dist;
graph[from].push_back({ to, dist });
graph[to].push_back({ from, dist });
}
dfs(1);
for (int i = 0; i < 2; i++)
{
memset(visited, 0, sizeof(visited));
dfs(startNode);
}
for (int i = 1; i <= N; i++)
cout << result[i] << "\n";
}
'알고리즘&자료구조 > 문제' 카테고리의 다른 글
| [프로그래머스] 요격시스템 (C++) (2) | 2023.07.08 |
|---|---|
| [BOJ/26154번] 한양 가왕 (C++/애드 혹) (2) | 2023.06.06 |
| [BOJ] 12865 평범한 배낭 C++ (2) | 2023.05.29 |
| [BOJ] 2564 경비원 C++ (0) | 2023.05.29 |
| [BOJ] 7490 0 만들기 C++ (0) | 2023.05.29 |