개요
회로에서 같은 동작을 한다면, 가급적 회로를 최소화 시켜 해야한다. (복잡성, 가격 등의 이유)
K-Map
True Table을 그림의 형태로 재구성하여 나타낸 표이다.
네모 칸들로 구성된 다이어그램이며, 각 칸은 최소화하고자 하는 함수의 하나의 최소항(minterm)을 나타낸다.
K-Map을 활용하면 훨씬 직관적으로 계산 가능하다.
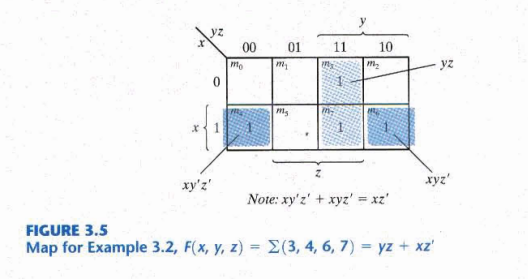
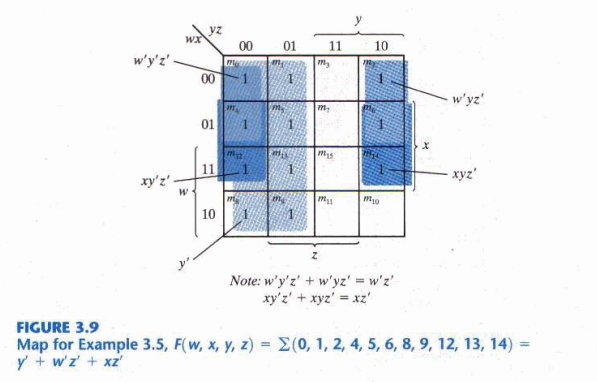
인접한 칸을 묶어서 간략화하는데, 2의 거듭제곱의 개수로 묶어야 한다.
양 끝 면은 서로 인접한 것으로 간주하고 묶어서 간략화할 수 있다.
주항(Prime Implicants)
주항은 Map에서 인접한 칸을 최대로 많이 묶을 때 생기는 곱의 항을 의미한다.
어떤 칸에 있는 항이 단 하나의 주항에 의해서만 커버된다면, 이 주항을 필수 주항(Essential PI)이라고한다.
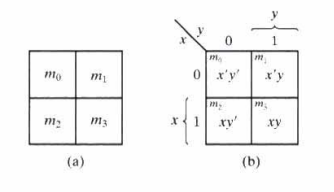
2-변수 맵(Two-Variable Map)

3-변수 맵(Three-Variable Map)

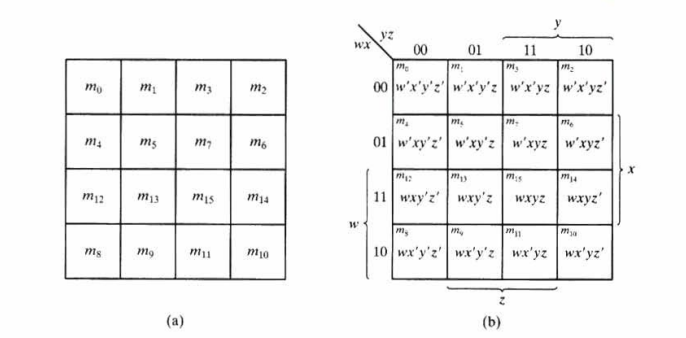
4-변수 맵(Four-Variable Map)
5-변수 맵(Five-Variable Map)
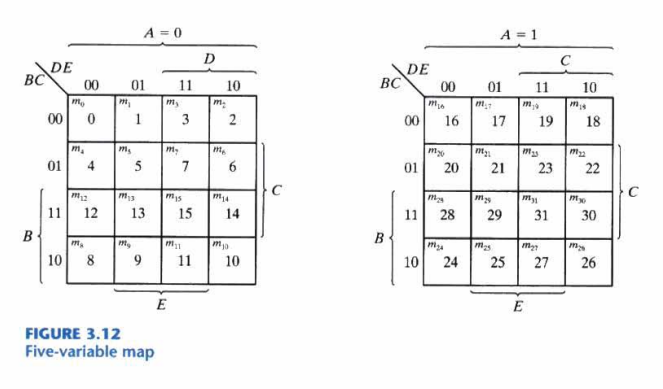

Four-Variable Map의 형태로 2개 그려 간략화한다.
인접 관계에 주의 . . . (2개의 맵이 z축으로 겹쳐있다고 생각하자)
Product of sum의 간략화


Sum of prosuct을 간략화 하는 방식에서 1이 아닌 0으로 간략화 하면 보수화된 함수를 도출해낼 수 있다.
드모르간 법칙을 적용하면 Product of sum 형식으로 간략화된 함수를 얻는다.
무 정의 조건(Don't care conditions)
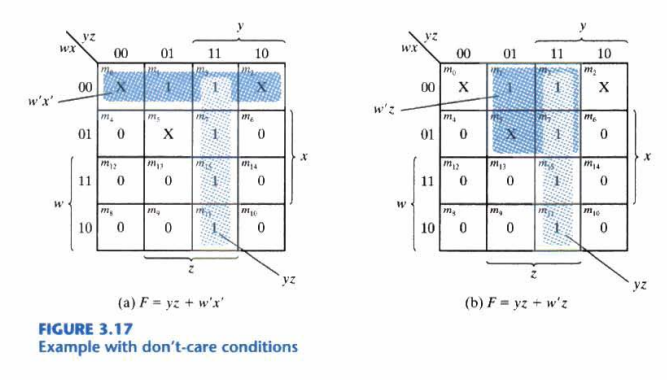
규정되지 않은 최소 항들을 don't care conditions라고 한다.
이는 간략화 과정에 있어서 포함해도, 포함하지 않아도 상관이 없다. (도움 되는 방향으로 활용)
참조
728x90