트리(Tree)
트리는 계층적 관계(Hierarchical Relationship)를 표현하는 비선형 자료구조이다.
트리를 만드는 도구를 만들어 놓으면 다양한 목적으로 활용이 가능하다.
트리의 관련 용어
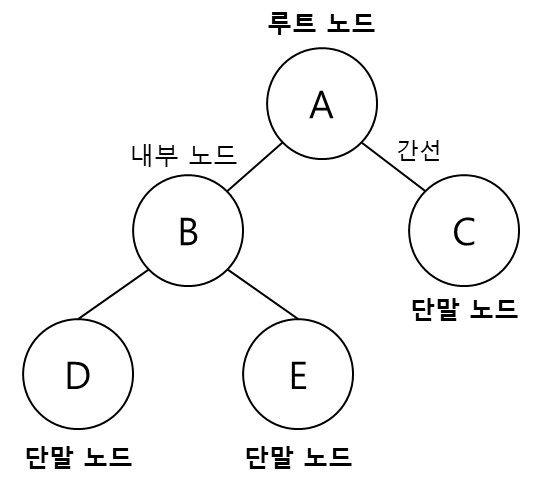


- 노드(node)
- 트리의 구성요소(A, B, C, D, E) - 간선(edge)
- 노드와 노드를 연결하는 선 - 루트 노드(root node)
- 트리 구조에서 최상위 노드(A) - 단말 노드(terminal node)
- 아래로 노드가 연결 되어 있지 않은 노드(C, D, E) - 내부 노드(internal node)
- 단말 노드를 제외한 모든 노드(A, B) - 부모 노드(parent node)
계층적 구조에서 위에 연결되어 있는 노드(A는 B,C의 부모 노드) - 자식 노드(child node)
계층적 구조에서 아래에 연결되어 있는 노드(B,C는 A의 자식 노드) - 형제 노드(sibling node)
계층적 구조에서 부모가 같은 노드(D, E는 형제 노드) - 레벨(level)
트리의 계층을 구분하는 단위, 루트 노드를 레벨 0으로 보고 아래 계층으로 갈 수록 증가한다. - 높이(height)
트리의 높이, 트리의 최대 레벨과 동일한 값을 가진다.
서브 트리(Sub tree)

하나의 트리를 구성하는 작은 트리를 서브 트리라고 한다.
서브 트리는 또다른 서브 트리를 가진다.
트리는 이처럼 재귀적인 구조를 가진다.
이진 트리(Binary tree)
루드 노드를 중심으로 두 개의 서브트리로 나뉘며, 나뉘어진 두 서브 트리도 모두 이진 트리인 구조이다.
위와 같이 트리는 재귀적인 사고와 구현이 필요하다.
공집합 노드(Empty set)

공집합도 이진 트리에서는 노드로 간주한다.
즉, 하나의 노드에 두 개를 초과하는 노드가 있지 않는 한 이진 트리로 간주한다.
완전 이진 트리(Complete binary Tree)
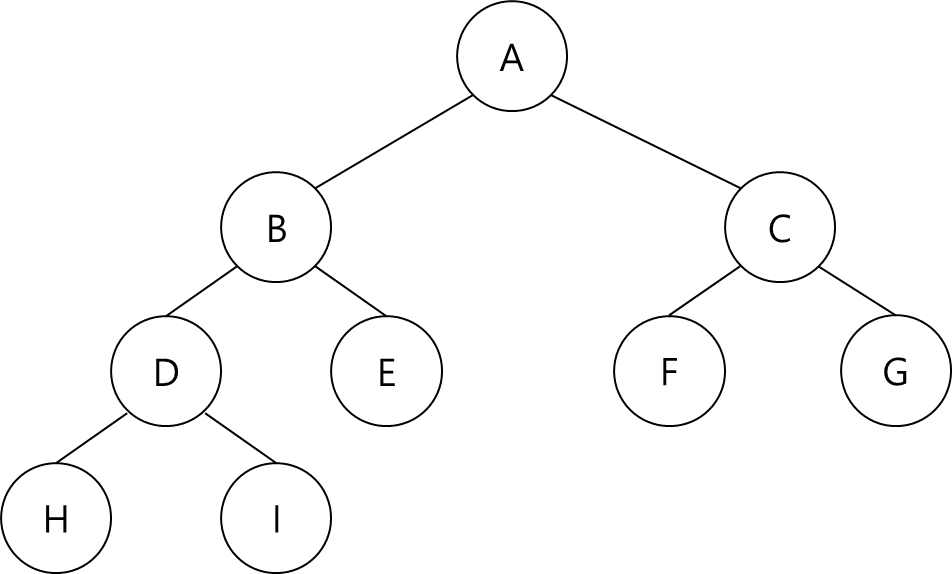
노드가 위에서 아래로, 왼쪽에서 오른쪽으로 순차적으로 채워진 트리를 뜻한다.
포화 이진 트리(Perfect binary tree)

모든 레벨이 채워진 트리를 뜻한다. 포화 이진 트리는 동시에 완전 이진 트리이기도 하다.
이진 트리 구현
크게 배열과 연결 리스트 기반의 구현이 있는데, 어떤 문제에 적용하느냐에 따라 잘 선택해서 활용해야 한다.
배열 구현

노드에 번호를 부여하여 인덱스 값으로 활용하는 방법이다.
편의상 첫 번째 요소는 사용하지 않는 것이 보편적이다.
연결 리스트 구현
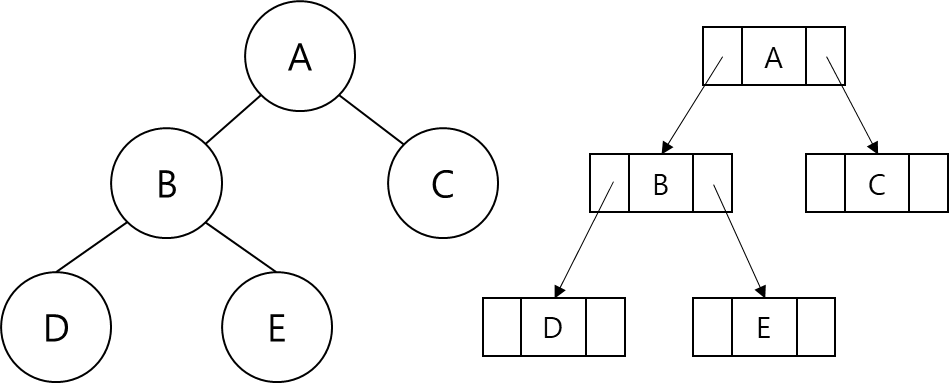
트리의 구조와 일치하여 직관적으로 이해하기 편하다.
이진 트리의 순회(Traversal)

루트 노드를 언제 방문하느냐에 따라 중위 순회, 후위 순회, 전위 순회로 나누어 진다.
재귀적으로 순회의 과정을 구성하면 된다.
수식 트리(Expression tree)
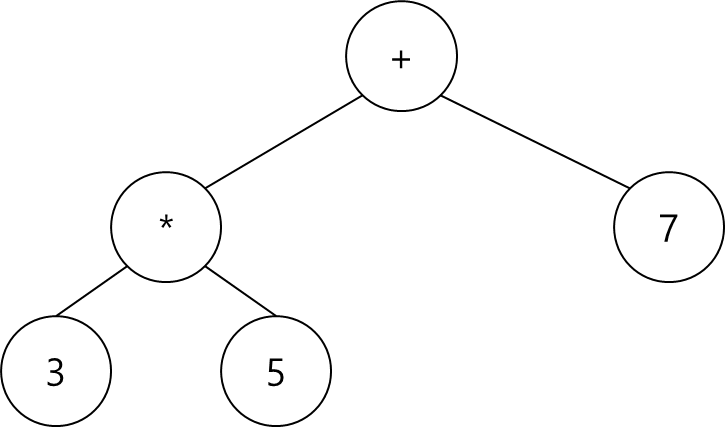
수식 트리는 수식을 표현하는 방법중 하나이다.
중위 표기법은 사람이 인식하기 좋은 방법이기 때문에 컴파일러는 중위 표기법을 수식 트리로 재구성한다.
중위 표기법을 수식 트리로 표현하는 것은 쉽지 않기 때문에 보통 후위 표기법으로 변환 후 수식 트리로 표현한다.
수식 트리 구현

수식 트리는 이진 트리와 스택으로 구현 가능하다.
피연산자는 스택에 넣고 연산자를 만나면 트리를 구성하면 된다.
구성된 트리를 다시 피연산자 취급하여 다시 스택에 넣고 위를 반복하면 된다.
참조
'알고리즘&자료구조 > 이론' 카테고리의 다른 글
| [알고리즘] 유니온 파인드(Union-FInd) (0) | 2023.02.23 |
|---|---|
| [알고리즘] 두 포인터 (Two Pointers) (1) | 2023.02.15 |
| [알고리즘] DFS와 BFS (0) | 2023.02.02 |
| [자료구조] 그래프(Graph) (0) | 2023.02.01 |
| [자료구조] 해시 테이블(Hash Table) (0) | 2022.10.21 |