DFS(Depth First Search)
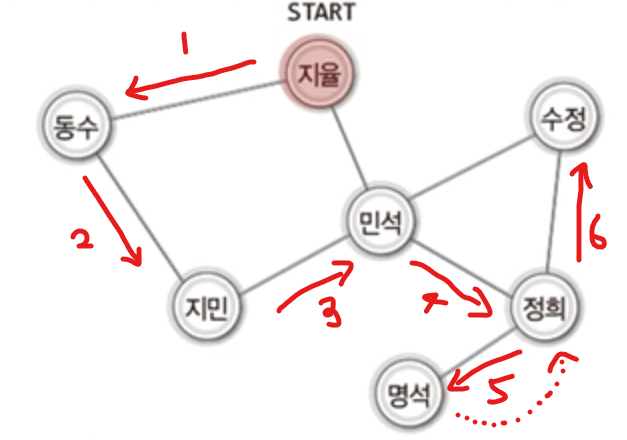
DFS(깊이 우선 탐색)는 그래프의 탐색 방법 중 한 가지이다.
DFS는 크게 세 가지 과정으로 나뉜다.
- 한쪽으로만 계속 방문
- 더 이상 방문할 정점이 없으면, 이전 정점으로 이동
- 처음 정점으로 돌아가면 탐색 종료
DFS의 구현
정점 방문 정보 기록을 목적으로 스택을 활용하면 된다.
방문 여부는 배열에 저장한다.
정점을 방문할 때 출발 정점을 스택에 PUSH 하면 된다.
이때 방문 여부는 출발 정점, 도착 정점 둘 다 처리한다.
더 이상 방문할 정점이 없을 경우 스택에서 POP 하면서 이전 정점으로 돌아가며 다시 확인하면 된다.
모든 정점을 방문했을 경우를 배열로 확인하여 탐색을 종료하면 끝이다.
- 다음 정점 방문 (스택에 이전 정점 추가, 둘 다 방문 배열 체크)
- 방문할 정점 없을 경우 스택을 통해 이전 정점으로 이동
- 모든 정점 방문 시 종료(스택이 비었을 때 방문할 정점 없을 경우)
BFS(Breadth First Search)

BFS(너비 우선 탐색)는 그래프의 탐색 방법 중 한가지이다.
BFS는 출발 정점에서 연결된 모든 정점을 찾아가는 방식이다.
다시 다음 정점에서 연결된 모든 정점을 찾아간다.
트리를 구성하는 느낌(?)하고 비슷하다.
- 출발 정점(A)에 연결된 모든 정점(B,C)을 방문
- 다시 그 정점(B, C)에서 연결된 모든 정점 방문
- 모든 정점 방문 시 탐색 종료
BFS의 구현
정점 방문 정보 기록을 목적으로 큐를 활용하면 된다.
방문 여부는 DFS와 마찬가지로 배열에 저장한다.
연결된 모든 정점을 enqueue한다.
dequeue를 수행하고 해당 정점의 모든 연결된 정점을 다시 enqueue한다.(방문하지 않은 정점만)
위를 반복하다 모두 탐색했을 경우(큐가 비었을 경우) 종료한다.
- 연결된 모든 정점 enqueue
- dequeue한 정점의 연결된 방문하지 않은 정점 enqueue
- 큐가 비었을 경우 탐색 종료
728x90
'알고리즘&자료구조 > 이론' 카테고리의 다른 글
| [C++/g++] PBDS(Policy Based Data Structure) (4) | 2023.11.20 |
|---|---|
| [알고리즘] 유니온 파인드(Union-FInd) (0) | 2023.02.23 |
| [알고리즘] 두 포인터 (Two Pointers) (1) | 2023.02.15 |
| [자료구조] 그래프(Graph) (0) | 2023.02.01 |
| [자료구조] 해시 테이블(Hash Table) (0) | 2022.10.21 |