개요
https://www.acmicpc.net/problem/10090
10090번: Counting Inversions
A permutation of integers from 1 to n is a sequence a1, a2, ..., an, such that each integer from 1 to n is appeared in the sequence exactly once. Two integers in а permutation form an inversion, when the bigger one is before the smaller one. As an example
www.acmicpc.net

알아두면 좋을 것 같은 유형 (P5)
본문
요약하면 순열에서 역전된 쌍의 개수를 찾는 문제이다.
N이 100만이기 때문에 나이브하게 접근하면 당연히 시간 초과다.
이 문제는 세그먼트 트리를 활용해 풀 수 있다.
우선 입력된 값을 인덱스로 사용하여 업데이트한다.
순열(2 4 3 1)을 예로 들겠다.

초기 상태의 트리이다.

2를 입력했다.
위와 같이 입력 값인 2에 대응하는 리프노드에 1을 체크해 주고 Range Sum으로 업데이트해 준다.

다음으로 4가 입력된다.
2는 4보다 작으므로 4역시 역전된 경우가 없다. 2와 같이 업데이트해 준다.
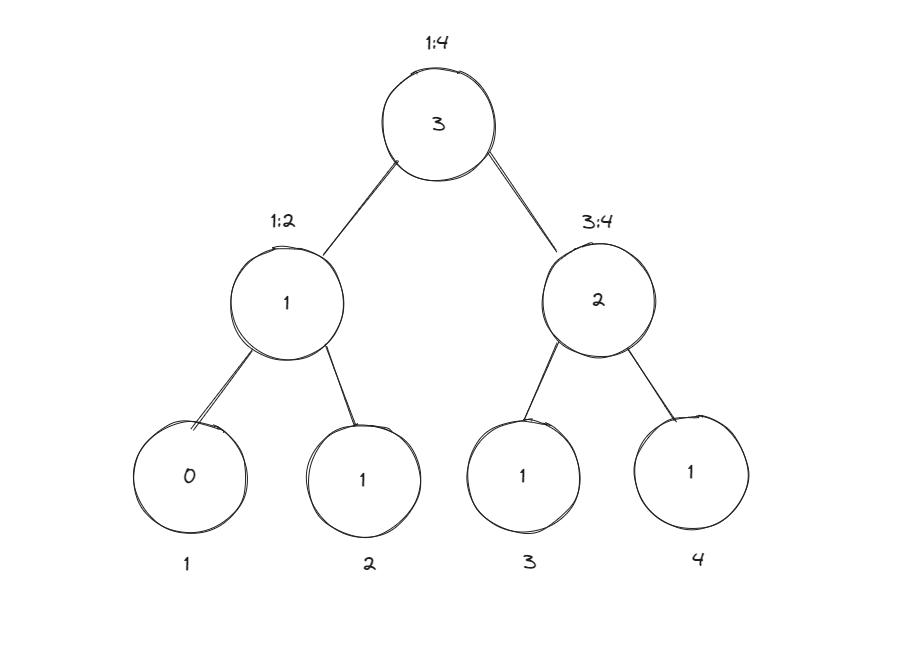
다음으로 3을 입력한다.
3은 2보단 크지만 4보단 작으므로 역전된 상태이다.
따라서 Result에 1을 더해주어야 한다.
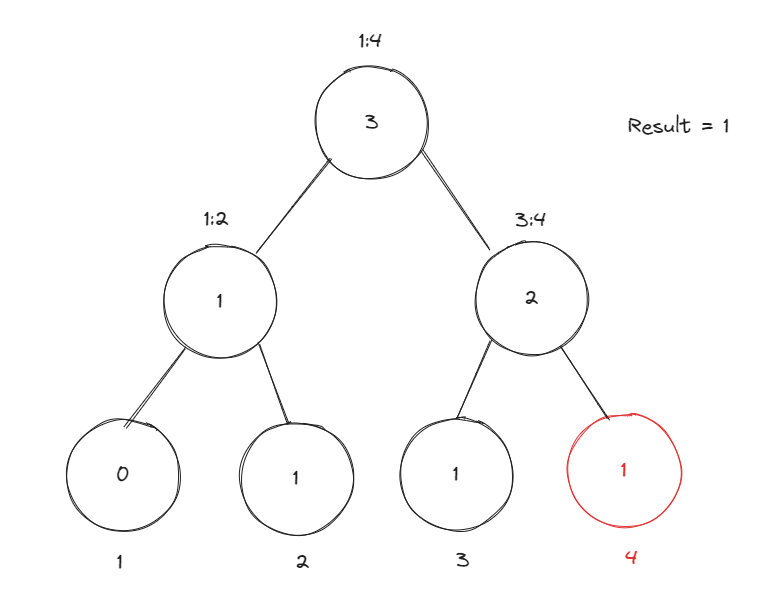
이는 3 + 1부터 N까지의 Range Sum을 쿼리로 실행해 주면 된다.
위와 같이 result에 [4:4] 값인 1이 더해진다.
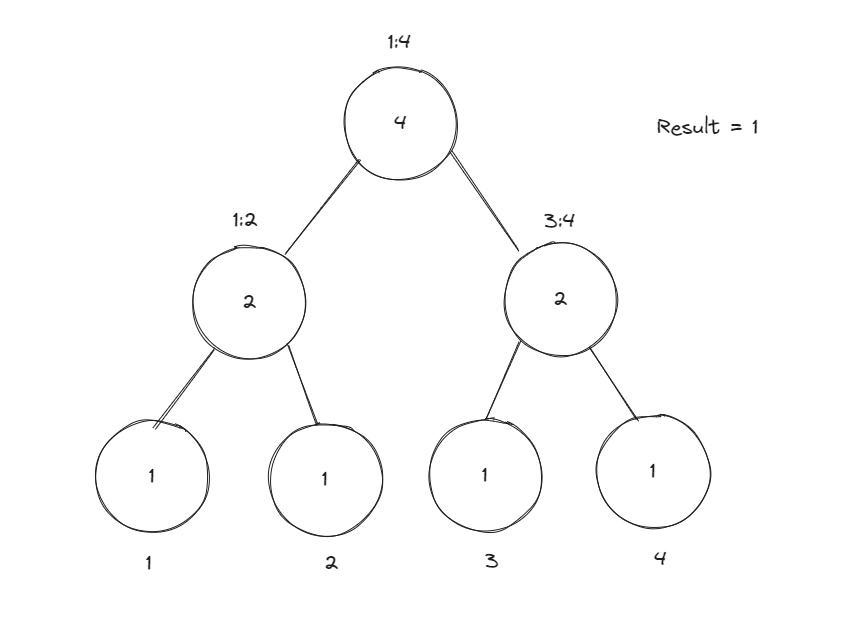
다음으로 1을 입력했다.
1은 2, 4, 3 보다 모두 작으므로 3쌍의 역전이 추가로 생긴다.
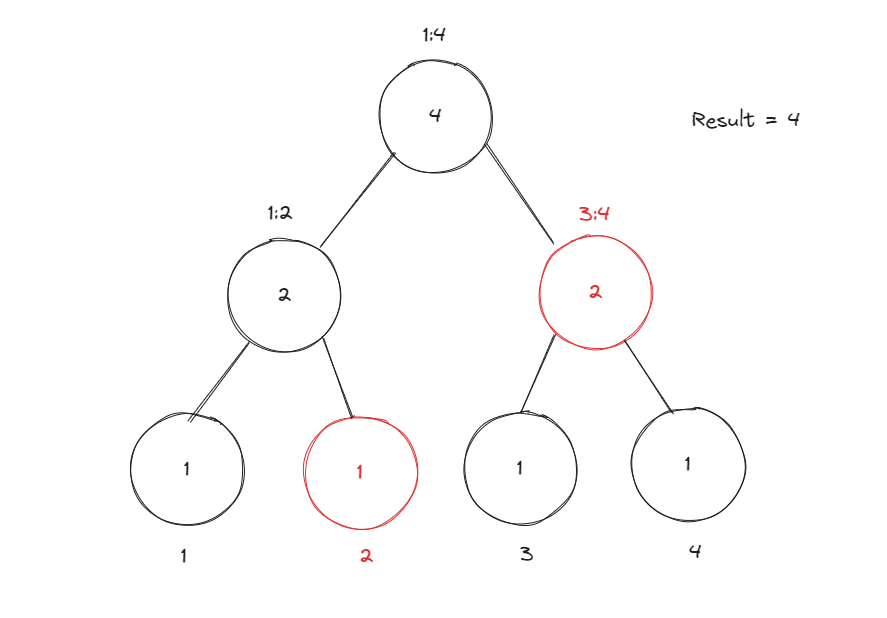
이전과 같이 [value+1 : N]의 쿼리를 실행하면 된다.
따라서 [2:4]의 값을 Result에 더하게 되며 이는 위와 같다.
따라서 순열 (2 4 3 1)은 총 4개의 역전된 쌍을 갖는다.
코드
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pi = pair<int, int>;
class segment_tree{
private:
vector<int> tree;
public:
segment_tree(int N){
int level = ceil(log2(N));
tree.resize(pow(2, level+1));
}
void update(int start, int end, int node, const int &val){
if(val < start || val > end) return;
if(start == end){
tree[node]++;
return;
}
int mid = (start + end) / 2;
update(start, mid, node*2, val);
update(mid+1, end, node*2+1, val);
tree[node] = tree[node*2] + tree[node*2+1];
}
int query(int start, int end, int node, const int &left, const int &right)
{
if(start > right || end < left) return 0;
if(start >= left && end <= right) return tree[node];
int mid = (start + end) / 2;
return query(start, mid, node*2, left, right) + query(mid+1, end, node*2+1, left, right);
}
};
int main()
{
cin.tie(0)->sync_with_stdio(0);
int n;
ll result = 0;
cin >> n;
segment_tree tree(n);
int a;
for(int i=1 ; i<=n; i++)
{
cin >> a;
tree.update(1, n, 1, a);
result += tree.query(1, n, 1, a+1, n);
}
cout << result;
}
'알고리즘&자료구조 > 문제' 카테고리의 다른 글
| [BOJ/2042] 구간 합 구하기 (C++) (1) | 2023.11.22 |
|---|---|
| [BOJ/3015] 오아시스 재결합 (C++) (2) | 2023.11.14 |
| [BOJ/22953번] 도도의 음식 준비 (C++/이분탐색) (1) | 2023.09.18 |
| [프로그래머스] 체육복 (C++) (0) | 2023.09.16 |
| [BOJ/2230번] 수 고르기 (C++/투포인터) (0) | 2023.09.16 |